GAMM Workshop on Numerical Analysis

RWTH Aachen University, November 1-2, 2017
Organizers: Daniel Peterseim, Lars Grasedyck ✉ (GAMM FA Numerical Analysis)
Local Organizers: Sebastian Kraemer ✉ , Christian Löbbert ✉, Dieter Moser ✉
This workshop is part of the foundation of the GAMM Activity Group on Numerical Analysis.
The focus lies on bringing together the young researchers from the field of Numerical Analysis.
Additional to the conference talks, a short course on the adaptive mesh refinement methods
is organized by Philipp Morgenstern
and Fleurianne Bertrand .
Find the full program here.
Registration:
Each participant may contribute a talk or a poster. For the registration please provide your name, affiliation, research topic and abstract to Dieter Moser ✉.Venue, Travel and Accommodation:
The workshop will take place in the RWTH Main Buildung (Templergraben 55) in room 149 on the first day and in the conference hall on the 6th floor of the RWTH Super-C Building (Templergraben 57) on the second day.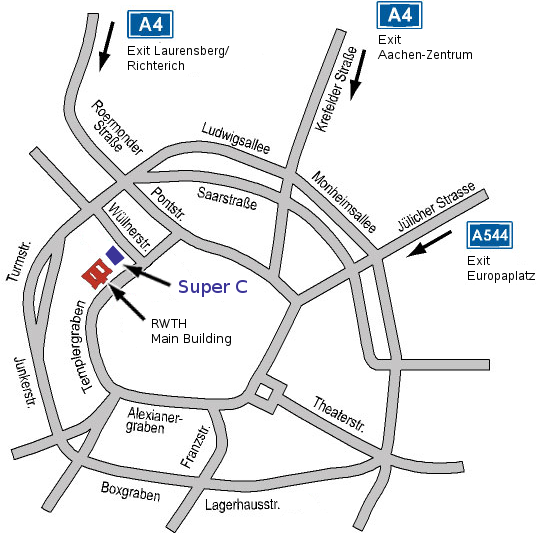
On the first day we will welcome you between 9:30 and 10:00 at the main entrance of the RWTH Main Building. Since we have to open and close the main entrance that day, we would like to let in as many participants as possible until 10:00.
If you will arrive later please send an email to Dieter Moser ✉ before arrival at the main entrance, so that we may let you in. The same procedure applies after lunch and the guided tour, between 15:20 and 15:30.
On the second day there will be no such restrictions and a nicer view.
Since the venue is on the campus site, eduroam is available in both venues.
Most Hotels are in a walking distance of 20 minutes, we recommend one of the following hotels:
- Aquis Grana City Hotel Büchel 32 / Buchkremerstraße
- IBIS Aachen Marschiertor / Friedlandstraße 6
- Novotel Aachen City / Peterstraße 66
For more touristic informations see "Aachen at a glance".
Program:
Wednesday, November 1st 2017
| 10:00 | Arrival and Introduction |
| 10:30 | Short Course (Pt. 1): Adaptive Finite Element Methods in Solid Mechanics: History and State Of
The Art Held by Gerhard Starke . |
| 12:00 | Lunch and Guided Tour |
| 15:30 | Short Course (Pt. 2):
High-performance algorithms for adaptive mesh refinement
Held by Carsten Burstedde |
| 17:00 | Coffee Break |
| 17:30 | Space-parameter-adaptive approximation of affine-parametric elliptic PDEs Held by Markus Bachmayr |
| 18:00 |
Rothe Discretization and Regularization of the Navier-Stokes equations
Held by Robert Altmann |
| 20:00 | Dinner |
Thursday, November 2nd 2017
| 10:00 | Meeting in the Super C conference hall (Templergraben 55, 6th floor) |
| 10:15 | GAMM Activity Group Numerical Analysis meeting |
| 11:00 | Pressure-robust finite element methods for the Navier-Stokes equations Held by Christian Merdon |
| 11:30 | Stable ALS Approximation in the TT-Format for Rank-Adaptive Tensor Completion
Held by Sebastian Krämer |
| 12:00 | Lunch Buffet and Poster Session |
| 14:00 | On the derivation of Cockburn and Shu's Discontinuous Galerkin scheme
Held by Sebastian Noelle |
| 14:30 | A Mixed Finite-Element Method for Gas Transport on Pipeline Networks
Held by Herbert Egger |
| 15:00 | Coffee Break |
| 15:30 | Perfectly matched layers for the linear Boltzmann equation
Held by Matthias Schlottbom |
| 16:30 | TBA |
| 17:00 | Farewell |
Abstracts
Short course
Adaptive Finite Element Methods in Solid Mechanics: History and State Of The Art
After several decades of intensive research, a posteriori error estimation and adaptivity are now established as core features of finite element methods. From the very beginning, this development was inspired by applications in solid mechanics where the accurate numerical simulation of elastic and inelastic deformation processes is usually not possible on quasi-uniform meshes. This talk will present some key issues of adaptivity and their development from the point of view of duality for variational formulations of elliptic problems. Variational inequalities arising, for example, in association with contact problems will also be discussed and some current research directions will be sketched in this context.Held by Gerhard Starke
High-performance algorithms for adaptive mesh refinement
A crucial task for the numerical solution of partial differential equations is to define the computational mesh and its partition among the processors. For many applications, it is desirable to perform all algorithms for adaptive mesh refinement (AMR) in parallel, that is, distributed between several (or rather many) computers, processors, processes, and/or threads. This applies for example to the refinement and coarsening of selected mesh elements and to the redistribution of mesh elements from one process to another (partitioning) in order to match the computational workload between them. Other operations are global in nature, for example to modify the mesh to satisfy consistency requirements between neighbor elements, say to adjust their sizes to each other.We are thus facing two problems: (1) the mathematical definition of an encoding and ordering of mesh elements that lets us identify, access, and modify the elements efficiently and (2) the distributed nature of a parallel computation in the sense that each process stores a small (local) part of the mesh in memory, yet it must be able to respect non-local conditions. Forest-of-octrees AMR is an approach that addresses both problems and has been successfully demonstrated in practice. To provide a functional and well-proven example, we present central data structures and algorithmic concepts from our research into the p4est and t8code software libraries. p4est is an implementation of adaptive hexahedra that is being used in several modern finite element codes. t8code is an effort that aims to unify hexahedral and tetrahedral tree-based AMR, introducing a new simplicial space filling curve. We close with illustrations from recent research into large-scale numerical simulations.
Held by and Carsten Burstedde
Talks
Pressure-robust finite element methods for the Navier-Stokes equations
Inf-sup stable mixed finite element methods for the steady incompressible Stokes equations that relax the divergence constraint lead to a pressure-dependence in the velocity approximation that scales with the inverse of the viscosity and so gives rise to a locking phenomenon. A recently proposed variational crime is able to restore the pressure-robustness for a large class of classical finite element methods without compromising convergence rates and inf-sup stability. This talk explains the necessary modifications and illustrates the superiority of the modified schemes compared to their classical siblings by a priori error analysis and numerical examples. Furthermore, some currently investigated aspects of the novel schemes are discussed.Held by Christian Merdon
Space-parameter-adaptive approximation of affine-parametric elliptic PDEs
We consider the approximation of PDEs with parameter-dependent coefficients by sparse polynomial approximations in the parametric variables combined with suitable discretizations in the spatial domain. Here we are especially interested in problems with countably many parameters, as they arise when coefficients with uncertainties are modelled as random fields. For the resulting fully discrete approximations of the corresponding solution maps, we obtain convergence rates in terms of the total number of degrees of freedom. In particular, in the case of affine parametrizations, we find that independent adaptive spatial approximation for each term in the polynomial expansion yields improved convergence rates. Moreover, we give a construction of near-optimal adaptive solvers for finding such approximations.Held by Markus Bachmayr
This talk is based on joint works with Albert Cohen, Wolfgang Dahmen, Dinh Dung, Giovanni Migliorati, and Christoph Schwab.
Rothe Discretization and Regularization of the Navier-Stokes equations
We start with a numerical example of a cylinder wake, discretizing first in time and then in space. This approach has the advantage that we may change (adaptively) the mesh in every time step. However, we observe that such grid changes lead to jumps in the error of the pressure variable. This is caused by the fact that the system generalizes a DAE of index 2. In order to prevent such instabilities, we present a regularization. This leads to an equivalent system, which is more robust in terms of perturbations, and eliminates the error jumps.Held by Robert Altmann
Perfectly matched layers for the linear Boltzmann equation
The linear Boltzmann equation is a hyperbolic integro-partial differential equation that describes the dynamics of a single-particle probability distribution in location-velocity phase space. The dynamics is governed by streaming, damping and scattering. The two main challenges in the numerical approximation of solutions to the linear Boltzmann equation are (i) the high dimensionality of the phase space, and (ii) the non-smoothness of the solution. The linear Boltzmann equation is equivalent to a mixed variational problem that incorporates boundary conditions naturally. However, the natural inclusion of boundary conditions introduces a non-smooth coupling of spatial and velocity variables, which is inconvenient for practical implementations. To overcome this difficulty, we introduce an absorbing layer and consider a perturbed problem such that the resulting variational problems exhibit a tensor-product structure.Held by Matthias Schlottbom (full abstract)
Stable ALS Approximation in the TT-Format for Rank-Adaptive Tensor Completion
Low rank tensor completion is a highly ill-posed inverse problem, particularly when the data model is not accurate, and some sort of regularization is required in order to solve it. In this article we focus on the calibration of the data model. For alternating optimization, we observe that existing rank adaption methods do not enable a continuous transition between manifolds of different ranks. We denote this flaw as instability (under truncation). As a consequence of this flaw, arbitrarily small changes in the singular values of an iterate can have arbitrarily large influence on the further reconstruction. We therefore introduce a singular value based regularization to the standard alternating least squares (ALS), which is motivated by averaging in micro-steps. We prove its stability and derive a natural semi-implicit rank adaption strategy. We further prove that the standard ALS micro-steps are only stable on manifolds of fixed ranks, and only around points that have what we define as internal tensor restricted isometry property iTRIP. Finally, we provide numerical examples that show improvements of the reconstruction quality up to orders of magnitude in the new Stable ALS Approximation (SALSA) compared to standard ALS.Held by Sebastian Krämer
A Mixed Finite-Element Method for Gas Transport on Pipeline Networks
We consider the simulation of gas transport through pipe networks. An appropriate mixed variational formulation is proposed to take into account the coupling conditions at pipe junctions automatically. This allows to obtain energy stable and mass conserving discretization schemes by Galerkin projection. A mixed finite element method is briefly discussed as a particular choice. We also discuss the preservation of further structural properties, like uniform exponential stability and the correct approximation of asymptotic regimes.Held by Herbert Egger
On the derivation of Cockburn and Shu's Discontinuous Galerkin scheme
In a landmark paper, Cockburn and Shu (Math. Comp. 1989) introduced the Runge-Kutta Discontinuous Galerkin (RKDG) method for hyperbolic systems of conservation laws. Together with the ENO and WENO schemes, the RKDG method is one of the most powerful and widely used high-order accurate methods for compressible flows. In this talk, we re-derive the RKDG scheme systematically from the weak formulation of conservation laws: we restricting the support of the test functions to a single space-time computational cell, and then pass to the semi-discrete limit. The result is, of course, the original scheme. But the new derivation fills two interesting gaps in the original argument by highlighting an infinitesimal version of the integral law at the cell edges, which survives the semi-discrete limit and guarantees consistency with the weak form. Our derivation leads to a new interpretation of the role of the numerical flux.Held by Sebastian Noelle
Poster
Quarkonial decompositions on domains
This poster is concerned with new discretization methods for the numerical treatment of elliptic partial differential equations. We derive an adaptive frame scheme that is based on quarkonial decompositions. These new frames are constructed from a finite set of functions by translation, dilation and multiplication by monomials. By means of nonoverlapping domain decompositions, we establish quarkonial frames on domains that can be decomposed into the union of parametric images of unit cubes. We also show that these new representation systems constitute stable frames in scales Sobolev spaces. The construction is performed in such a way that, similar to the wavelet setting, the frame elements, the so-called quarklets, possess a certain amount of vanishing moments. This enables us to generalize the basic building blocks of adaptive wavelet algorithms to the quarklet case. The applicability of the new approach is demonstrated by numerical experiments for the Poisson equation on L-shaped domains.Presented by Alexander Sieber and Philipp Keding

