Mathematical Models
Navier-Stokes Equations
In each phase of the two-phase problem the flow is described by the instationary Navier-Stokes equations:
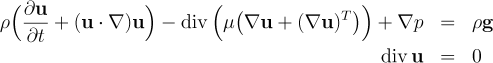
The density and the viscosity are constant, but differ for the two phases. In addition suitable initial and boundary conditions are needed.
Notation: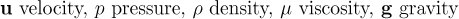
Continuum Surface Force
A standard assumption is that the surface tension balances the stress at the phase-interface. This can be modeled by a force localized at the interface, using the so-called continuum surface force (CSF) technique:
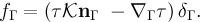
This term is added as a force term in the momentum equation of the Navier-Stokes equations.
Notation: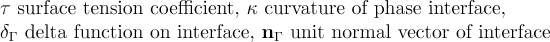
Mass Transport
The concentration of a dissolved species in one or both phases, that is transported due to convection and diffusion and does not adhere to the interface, can be modeled by the convection-diffusion equation for the concentration
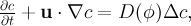
At the interface we need interface conditions
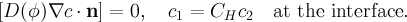
Notation:
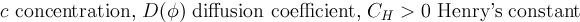
Surfactant
The concentration of a surfactant at the interface, can be modeled by the transport equation for the concentration
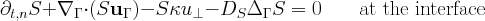
Notation:
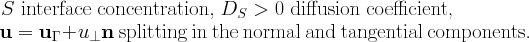
Numerical Methods
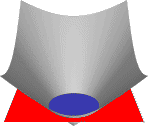
Level Set
The interface between the two phases is captured by a so-called level
set function
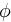 : :
|
|
Fast Marching
| For numerical and algorithmic purposes it is necessary to keep the level set function close to a signed distance function during the time evolution. We accomplish this by a reinitialization of the level set function using a variant of the Fast Marching method. |

|

|
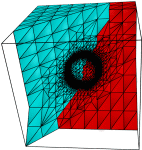
Adaptive Tetrahedral Grid Hierarchy
|
The spatial discretization is based on a hierarchy of tetrahedral
grids. The grids are consistent, i.e. there are no hanging nodes.
An important property is that local refinement and coarsening are
easy to realize. The local refinement is crucial for an accurate and efficient approximation of the interface. The hierarchical structure is exploited by the multi-level solvers. |
|
Refinement Algorithm
|
To ensure consistency of the grids, the refinement pattern of adjacent
tetrahedra has to match on common faces and edges. For this purpose DROPS
provides a regular refinement pattern (with all six edges refined) for a
tetrahedron and 63 irregular patterns for each possible pattern on the
edges. The patterns are chosen such that matching patterns on the edges
imply matching patterns on the faces. The rule that no irregular pattern can be refined (but has to be replaced by the regular pattern that can be refined instead) guarantees that the hierarchy of triangulations is stable. That means that the tetrahedra will not degenerate, i.e. all angles are uniformly bounded away from 0° and 180°. |

|
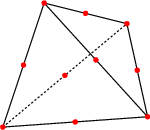
Finite Elements
|
For the discretization of velocity, pressure and the level set
function conforming finite elements are used. The Hood-Taylor
P2-P1 finite element pair is used
for velocity / pressure and the P2 finite element
is used for the level set function. We introduced an extended finite element (XFE) space for the pressure which is suited to represent functions which are discontinuous across the interface. For such functions this XFE method has a better approximation property of order 2 instead of order 1/2 for standard finite element spaces. |
|
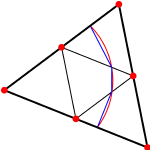
Curvature Approximation via Laplace-Beltrami
|
The CSF term contains two parts that should not be handled naively:
the delta function and the curvature (which is essentially a second
derivative). To eliminate the delta function, the integral of the
weak formulation is written as surface integral over the phase
interface. The second derivative introduced by the curvature can be
interpreted as a Laplace-Beltrami operator. In the weak formulation
the second derivative is transferred to the test function by a variant
of partial integration for surfaces. To approximate the resulting surface integrals, which only contain first derivatives, a piecewise linear reconstruction of the 0-level of the piecewise quadratic level set function on a finer grid is used. |
|
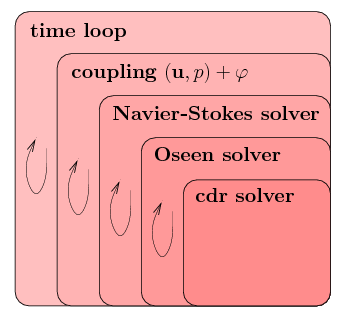
Nested Solvers
The instationary, non-linear and strongly coupled nature of the mathematical problem is mirrored in the structure of the solvers:
|
|
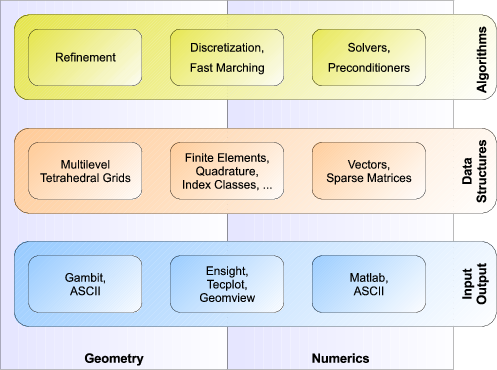
Software Design
Object-oriented Paradigm
DROPS is written in C++, making heavy use of the object-oriented features of the programming language. This holds especially for the nested solvers with its preconditioners, smoothers etc. In order not to sacrifice speed only compile-time polymorphism is used.
Data Structures
In DROPS there's a strict separation between the data structures for the geometry related data and the linear algebra related ones. This simplifies the algorithms (in particular solvers) and allows for high performance (lean data structures for positive cache effects which are optimized for fast matrix-vector multiplication).
DROPS has special data structures for all types of simplices in the grid, i.e. vertices, edges, faces, and tetrahedra. Nodes of different types of finite elements can therefore easily be associated with the respective simplices.
Vectors are based on the valarray class in C++. This allows
DROPS to use simple notations while not sacrificing performance due to
the implementation of valarray via expression templates.
For the sparse matrices DROPS uses a compact row-oriented storage format
that only stores the non-zero entries. During assembly of these matrices
an intermediate storage format is used as insertion of entries into the
final format is not cheap.
The vectors and matrices are connected to the geometric structure via index classes. These are used for example during assembly of the linear systems. Other important classes for the assembly are classes that represent single finite elements and classes that perform quadrature on them.
Grid Generation and Visualization
For the generation of the initial grid DROPS relies on external software. The data format used by the GAMBIT grid generator can be imported.
DROPS supports several software packages for visualization: Ensight, Tecplot, and Geomview. For further data processing ASCII output is available.
Overall Structure
|
Sven Groß ✉, last update: February 24th, 2008


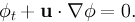
 -scheme.
-scheme.