SFB 540

The goal of the Collaborative Research Center SFB 540 "Model-based experimental analysis of kinetic phenomena in fluid multi-phase reactive systems" is the development of a new methodology (MEXA for short) for the systematic modeling of kinetic phenomena in fluid multi-phase reactive systems.

To reach this goal, activities such as process measurement, modeling, numerical simulation and solution of inverse problems, which have so far been conducted separately, are coordinated and combined into one work process. This leads to an improved physical understanding and a sufficiently accurate predictive mathematical model. 		SFB logo

Drops

The goals of this Collaborative Research Center pose several requirements on the software for the numerical simulations. Flexibility is needed to incorporate new mathematical models easily and accuracy to discriminate between different models. Especially for inverse problems high performance and robustness are vital ingredients.

These demands led to the development of the CFD software package DROPS for the simulation of incompressible two-phase flows. DROPS is based on state-of-the-art numerical techniques and an object-oriented software design to accomplish its task.

Within the Collaborative Research Center DROPS is currently used and developed in project B4 and C7 (former C6). For solving inverse problems derivatives of the results with respect to selected input data are necessary. Project C5 will provide these via automatic differentiation of the code.


Project B4

The main topic of project B4 "Multigrid Methods for the Numerical Simulation of Reactive Multi-phase Fluid Flow Models" is the simulation of a droplet in a surrounding fluid.

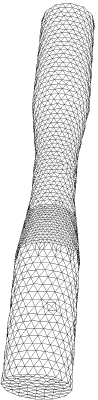
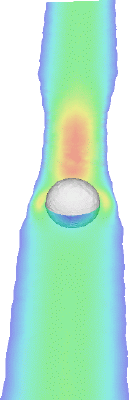
For physical experiments a droplet is levitated in a measuring cell: A fluid flows through the cell from top to bottom. A conical shaped part in the middle of the cell causes a velocity gradient of the flow. A droplet of a fluid of lower density rises up to the conical part of the measuring cell until the buoyancy forces balance the flow resistance.

The images show the droplet at the equilibrium position of the measuring cell, the grid used for the simulation, and the result of the simulation.

droplet in measuring cell grid for measuring cell simulated flow


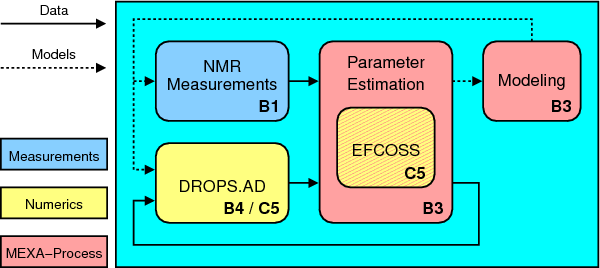
Project Group "Levitated Droplet"

Project B4 is embedded in the group "Levitated Droplet" which investigates phenomena related to the phase interface of the droplet.

  • Project B3 is responsible for the modeling of the phenomena, the experimental design, and the parameter estimation where experimental and simulated data are combined.
  • Project B1 performs the NMR measurements in the measuring cell.
  • Project B4 develops DROPS to simulate the models from B3.
  • Project C5 provides the tool EFCOSS for the solution of the inverse problems that need to be solved for the parameter estimation. The derivatives needed for the optimization process are generated by automatic differentiation of DROPS (resulting in DROPS.AD), which is also performed by C5.
structure of group B


Project C6

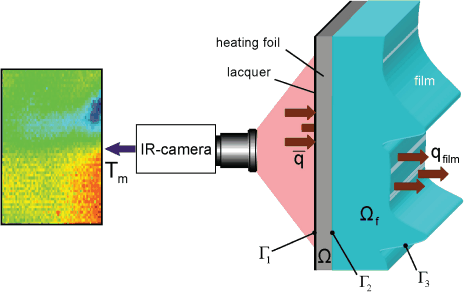
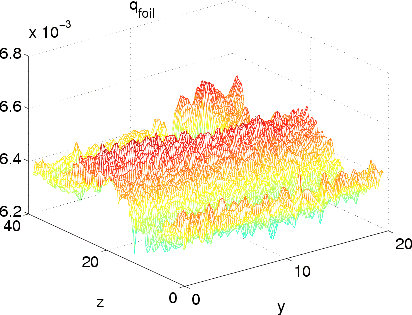
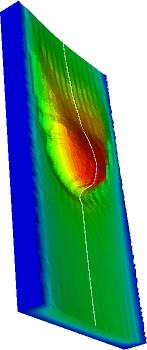
In project C6 "Adaptive Parameter Estimation Methods for Flow Problems" inverse heat conduction problems in wavy falling films are solved to estimate heat fluxes and heat transfer coefficients from high resolution temperature measurements. In this framework the DROPS package is used for solving the direct heat conduction problem and calculating the gradients via an adjoint problem inside the optimization loop.

The images show the experimental setup for the temperature measurements of the falling film with measured temperature profile and estimated heat flux.

film experiment with temperature profile
heat flux


Project C7

The project C7 "Development of Numerical Methods for the 3D Simulation of Wavy Falling Films" is devoted to the development of numerical methods for two-phase flow simulations of falling films and for the simulation of heat and mass transport inside the film and across the phase interface. High jumps in the material coefficients of the liquid-gas system (a factor of about 1000 for density and dynamic viscosity) as well as the dynamic phase interface with its large extent are the main challenges for the numerical treatment of the film problem.

The images show the numerical result for two examples of the falling film flow.

film flow


Project Group "Falling Films"

Projects C6 and C7 are embedded in the group "Falling Films", which investigates the transport of momentum, heat and mass in wavy falling films.

  • Project C2: modeling and simulation of transport phenomena (momentum, heat, mass)
  • Project C3: measurements of momentum and heat transport
  • Project C4: measurements of mass transport
  • Project C5: tool EFCOSS for the solution of inverse problems, used for estimation of few parameters
  • Project C6: solution of inverse heat conduction problems (model-free estimation in 3D)
  • Project C7: development of numerical methods for 3D-simulation of momentum, heat and mass transport



Sven Groß ✉, last update: February 24th, 2008